Algebra Equations That Equal 10

An algebraic equation can be defined equally a mathematical statement in which two expressions are set equal to each other.The algebraic equation usually consists of a variable, coefficients and constants.

Also Check: Algebraic Expressions .

In unproblematic words, equations mean equality i.east. the equal sign. That's what equations are all nearly- "equating one quantity with another".

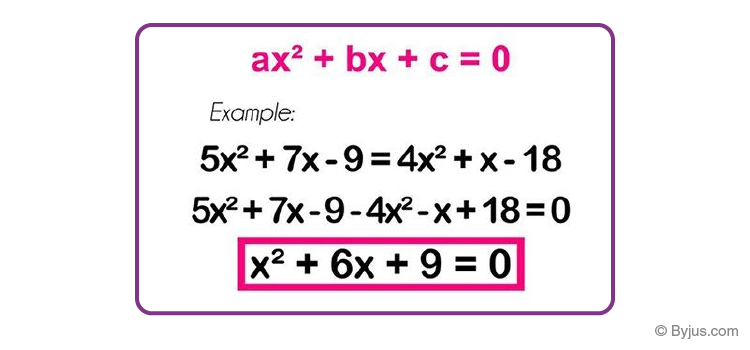
Algebraic Equations

Equations are like a balance scale. If you've seen a balance scale, you lot would know that an equal amount of weight has to be placed on either side for the scale to exist considered "balanced". If we add some weight to only ane side, the calibration will tip on one side and the two sides are no longer in residual. Equations follow the same logic. Whatever is on one side of the equal sign must have exactly the aforementioned value on the other side else it becomes an inequality.

Table of contents:

Definition
What is an equation?
Types of Algebraic equations
- Polynomial Equations
- Quadratic Equations
- Cubic Equations
- Rational polynomial Equations
- Trigonometric Equations
How to Solve Algebraic Equations
Solved Examples
Departure betwixt equation and expression
FAQs

What are Algebraic Equations?

An algebraic equation is an equation in the grade:

P = 0

Where P is a polynomial.

For case, ten + viii = 0 is an algebraic equation, where ten + 8 is a polynomial. Hence, information technology is also called a polynomial equation.

An algebraic equation is always a balanced equation that includes variables, coefficients, and constants.

Consider an equation ane+one = 2.

It is balanced as both sides have the aforementioned value. To avert committing an error that tips the equation out of balance, brand sure that any change on one side of the equation is reciprocated on the other side. For example, if you want to add a number v to i side of the equation y'all volition have to add the same five to the other side of the equation i.e.

1 + i = 2

1 + 1 + v = two + 5

The same goes for subtraction, multiplication, and division. Every bit long every bit you do the same thing to both sides of the equation information technology volition remain balanced.

What is an Equation?

An equation is simply divers as mathematical statements that express the relationship betwixt two values. Usually, the two values are equated past an equal sign in an equation.

For example, 2x+3 = 7 is an equation, where 2x+3 and seven are equated by equal to "=" sign.

2x+3 is at the Left-manus side of the equation and 7 is at the right-hand side. In this example,

2x, 3 and 7 are terms
x is the variable
3 and seven are the constants
'+' is the operator

If we write ten = iii, then it is also an equation, where we are denoting the value of variable ten equal to 3.

Types of Algebraic Equations

Algebraic equations are of various types. A few of the equations in algebra are:

Polynomial Equations
Quadratic Equations
Cubic Equations
Rational polynomial Equations
Trigonometric Equations

Polynomial Equations

All the polynomial equations are a part of algebraic equations like the linear equations. To recall, a polynomial equation is an equation consisting of variables, exponents and coefficients.

Linear equations: ax+b=c (a not equal to 0)

Quadratic Equations

A quadratic equation is a polynomial equation of caste ii in one variable of type f(x) = axⁱⁱ + bx + c.

Quadratic Equations: ax^two+bx+c=0 (a not equal to 0)

Cubic Equations

The cubic polynomials are polynomials with degree 3. All the cubic polynomials are also algebraic equations.

Cubic Polynomials: ax³+bx²+cx+d=0

Rational Polynomial Equations

P(x)/Q(x)=0

Trigonometric Equations

All the trigonometric equations are all considered as algebraic functions. For a trigonometry equation, the expression includes the trigonometric functions of a variable.

Trigonometric Equations: cos2x = 1+4sinx

How to Solve Algebraic Equations

Consider the following situation. I am going on a trip. In one pocketbook I carry some t-shirts, shorts, and towels. A total of 8 items can fit in the purse. So I pack 4 shirts and two shorts. How many towels can I now carry?

Consider the number of towels to exist '10'. Let's grade the equation at present.

4 shirts + ii shorts + 'x' towels = viii clothes

The left-paw side (LHS) of our equation is existence compared to the right-hand side (RHS) of the equation.

Now, let'southward solve this equation:

4+two+ten=8

6+10=8

half-dozen+x-six=8−6

ten=two

I can behave 2 towels for my trip.

In the same way, what would depict an inequality? Evidently, when the left-mitt side is not equal to the right-hand side. How would this happen?

Permit's take the aforementioned 6 + x = 8 and modify that equal to into a greater than or a lesser than sign. These aren't equations! Consider some examples to clarify this concept.

x + ii = 21, xy + nine = z are equations but 6p > 77 is not.

Acquire More: Solving Linear Equations

Solved Examples

Q.one: Simplify the given equation : 2(x+four)+3(x–v)–2y=0

Solution:

Given equation: 2(x+4)+iii(x−5)–2y=0

2x+2×4+3x–3×5–2y=0 (Using Distributive property to get rid of parenthesis)

2x+8+3x–fifteen–2y=0 (Simplifying)

5x–2y–7=0 (on further simplifying terms)

Q.two: Solve 10 + 1 = 9

Solution: Given, 10+i = 9

If we bring i from LHS to RHS, and then the sign of i volition get change.

x = nine – 1

x = viii

Hence, is the solution.

Q.3: Solve 15 + 5x = 0.

Solution: Given, 15 + 5x = 0

We need to solve for x here.

Let the term with x remain on the LHS and move the rest terms to the RHS.

5x = 0 – 15

5x = -15

Now split up both the sides past 5.

(5x)/v = -fifteen/five

x = -3

Thus, ten = -3 is the required solution.

Q.4: Solve -10x – 19 = xix – 8x

Solution: Given, -10x – 19 = nineteen – 8x is the algebraic equation.

Nosotros need to solve the given equation for x.

First write the terms with x on one side and other terms on the other side. Thus, we will add together 8x to both the sides

-10 10 -19 + 8x = 19 – 8x + 8x

At present group the like terms.

-10x + 8x – 19 = 19

-2x – xix = 19

Now add nineteen both the sides.

-2x – xix + 19 = 19 + 19

-2x = 38

Carve up both sides by two

(-2x)/2 = 38/2

-x = 19

Multiply both sides by -1

-x (-1) = 19 (-one)

x = -xix

Therefore, x = -19 is the required solution.

Departure Between Expression and Equations

Many times students are confused between expressions and equation. Here is the difference between them

Divergence Between Expression and Equations in Algebra

Frequently Asked Questions – FAQs

What are algebraic Equations?

An algebraic equation is a mathematical sentence, when two algebraic expressions are related with an equality sign (=). For example, 3x+6 = one is an algebraic equation.

What are the basics of algebra?

The basics of algebra include the mathematical operations such equally improver, subtraction, multiplication and sectionalisation. These operations are performed on equations consisting of variables and constants.

Is 10 an algebraic expression?

No, because an algebraic expression should have a variable.

How to Simplify Algebraic equations?

Follow the below steps to solve algebraic equations:
Remove the brackets or parentheses () and multiply the factors
Combine the similar terms and simplify them by adding or subtracting
Combine the constants and simplify them by adding or subtracting

What are the basic rules of algebra?

The bones rules or laws of algebra are:
Commutative constabulary ⇒ [ten+y = y+ten and x.y = y.10] Associative constabulary ⇒ [10+(y+z) = (ten+y)+z and 10.(y.z) = (ten.y).z] Distributive police ⇒ [x.(y+z) = ten.y + x.z]